INTRODUCTION TO A.I.

Fuzzy Logic

Lecture 9

March 15, 2007

9.1	Outline of Topics
	Formal Languages & Their Ontological and Epistemological Commitments
	Fuzzy Logic Overview
	Fuzzy Set Theory
	IF-THEN Rules / Fuzzy Inference
	Fuzzy Controler Example
	Example Computation
	Fuzzy Logic: Pros and Cons

9.2	Formal Languages & Their Ontological and Epistemological Commitments (see pp. 166 & 463 in your textbook)
	LANGUAGE	ONTOLOGICAL COMMITMENT (types of entities in the world)	EPISTEMOLOGICAL COMMITMENT (types of beliefs about entities)
	Propositional logic	facts	true/false/unknown
	First-order logic	facts, objects, relations	true/false/unknown
	Temporal logic	facts, objects, relations, times	true/false/unknown
	Probability theory	facts	degree of belief [0, 1] (probability)
	Fuzzy logic	degree of truth	degree of belief [0, 1]

9.3	Fuzzy Logic Overview
	What it is	A method for classification and decision making using a continuous scale of truthness/membership. An alternative to traditional notions of set membership. Superset of standard Boolean logic.
	History	Created by Lotfi Zadeh - 1965 paper on fuzzy sets. 1973 paper on the analysis of complex systems and decision processes. 1979 report and 1981 paper on possibility theory and soft data analysis.
	What it is composed of	Fuzzy sets & fuzzy membership rules IF-THEN rules
	Usage	Gained popularity in the late 1980s, esp. in Japan, as Japanese manufacturers started applying it to various kinds of control tasks in products such as cameras, washing machines and automobiles.

9.4	Fuzzy Set Theory
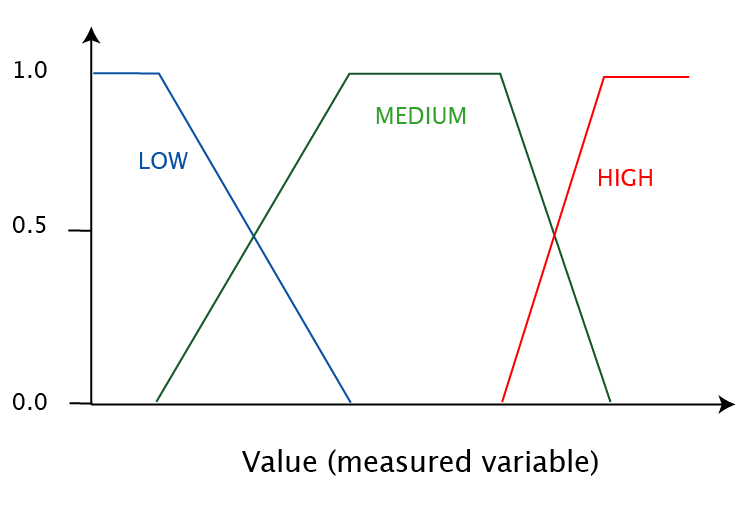
	What it is	A means of specifying how well an object satisfies a vague description, using a range from 0 to 1.
	Historically	Extensions of mathematical set theory as first studied by Cantor (1845-1918).
	Fuzzy membership	The proposition "the Sinclair Z80 is not a powerful computer " refers to an object (computer of type Z80) and classifies it into a set with other objects that can be considered/labeled "powerful".
	Notation	mPOWERFUL(Z80) = 0.1
	Examples	Driving FAST Jumping HIGH Steak is MEDIUM RARE John is BRILLIANT This math is EASY

Membership functions can be drawn in various ways. In the case of computer CPU speed, for example,
the low end of the x-axis would represent kHz and the high end GHz.

9.5

IF-THEN Rules

IF speed is HIGH & distance to next car is SMALL

THEN brake HARD

IF speed is HIGH & distance to next car is MEDIUM

THEN apply MEDIUM force to brake

IF speed is MEDIUM & distance to next car is MEDIUM

THEN apply MEDIUM force to brake

Speed:	HIGH	MEDIUM	LOW
distance: LARGE
MEDIUM
SMALL

Table representing permutations of measured variables' states

9.6	Fuzzy Inference
	T(A ∧ B)	= MIN(T(A), T(B))
	T(A ∨ B)	= MAX(T(A), T(B))
	T(¬A)	= 1 - T(A)
		...where T returns degree of truth (fuzzy membership)

	Mnemonic	AND = MIN / OR = MAX

9.7

Fuzzy Controler Example

Control task

Given that we are driving and we want to maintain a safe distance between us and the cars in front, how can we determine brake force based on our own speed and the distance to the car in front?

Create matrix / ruleset describing conditions and actions

Represented in a Matrix

Speed:	LOW	MEDIUM	HIGH
Distance: LARGE	0	0	1
MEDIUM	0	1	2
SMALL	1	2	2

Martix representing action to be taken in a fuzzy controller: Applied brake force (0, 1, 2).
Distance = distance between your car and the car in front of you.

Written As Rules

IF Speed is {LOW | MEDIUM} & Distance is LARGE
THEN brake force = 0

IF Speed is HIGH & Distance is LARGE
THEN brake force = 1

IF Speed is LOW & Distance is MEDIUM
THEN brake force = 0

IF Speed is MEDIUM & Distance is MEDIUM
THEN brake force = 1

IF Speed is HIGH & Distance is MEDIUM
THEN brake force = 2

IF Speed is LOW & Distance is SMALL
THEN brake force = 1

IF Speed is {MEDIUM | HIGH} & Distance is SMALL
THEN brake force = 2

9.8	Example Computation
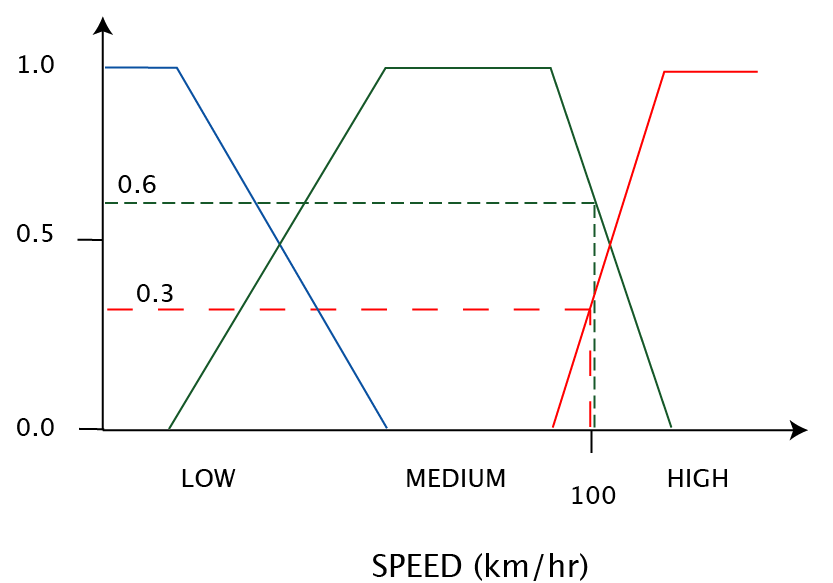
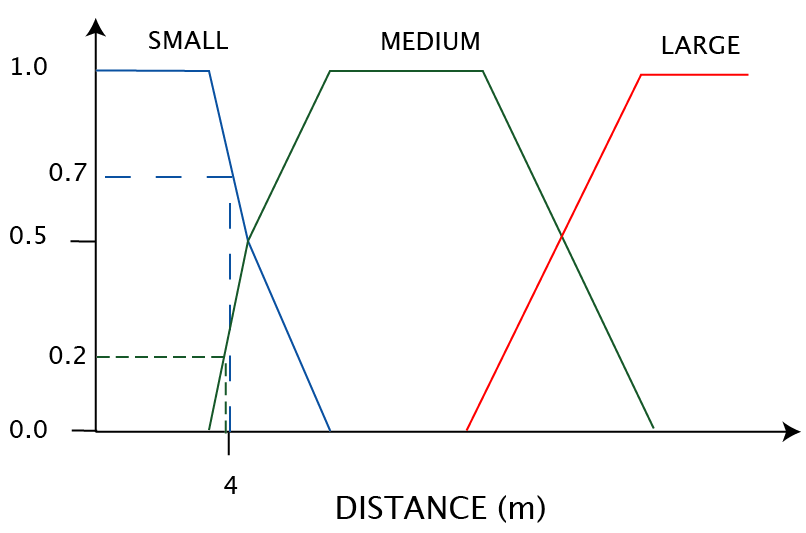
	Control task - specific case	Given that we are driving at 100 km/hr and there are 4 meters between us and the car in front, how hard should we hit the brakes?
	Given	Speed = 100km/hr Distance = 4 m
	Use rules to derive fuzzy membership and pick action

	WRITTEN AS RULES	FUZZY MEMBERSHIP (see graphs below)
1	IF Speed is {LOW \| MEDIUM} & Distance is LARGE THEN brake force = 0	min( (max[0, 0] = 0) & min([0]) ) = 0
2	IF Speed is HIGH & Distance is LARGE THEN brake force = 1	min[0.6, 0] = 0
3	IF Speed is LOW & Distance is MEDIUM THEN brake force = 0	min[0, 0.2] = 0
4	IF Speed is MEDIUM & Distance is MEDIUM THEN brake force = 1	min[0.3, 0.2] = 0.2
5	IF Speed is HIGH & Distance is MEDIUM THEN brake force = 2	min[0.6, 0.2] = 0.2
6	IF Speed is LOW & Distance is SMALL THEN brake force = 1	min[0, 0.7] = 0
7	IF Speed is {MEDIUM \| HIGH} & Distance is SMALL THEN brake force = 2	min( (max[0.3, 0.6] = 0.6 ) & (min[0.7]) ) = 0.6

	Pick the rule with the highest membership value	RULE 7: Brake force 2

9.9	Fuzzy Logic: Pros and Cons
	Pros	Simpler to use than most alternatives for solving complex control tasks (and often performs better). Very successful industrial applications: Autonomous subway in Tokyo washing machine control autofocus applications the MASSIVE autonomy engine used in the Lord of the Rings films etc.
	Cons	Need to be crafted by hand (although parameters can be subsequently tuned later by automatic learning techniques). May not scale well to large rulesets (i.e. same limitation as other kinds of rule-based knowledgebases).