BiSC is an algorithm inspired by a question asked by Sara Billey in the talk Consequences of the Lakshmibai-Sandhya Theorem at the AWM Anniversary Conference in 2011. She asked whether one could write an algorithm for "learning marked mesh patterns". The BiSC algorithm answers this question for mesh patterns. The name of the algorithm comes from the last name of Sara Billey, as well as the last names of Einar Steingrímsson and Anders Claesson who where also influential in the development of the algorithm.

Below you can download an implementation of BiSC in the computer algebra system Sage. What follows are instructions for using the algorithm. Please contact me via email if you find any bugs, want any clarifications or to suggest new features.

Download the program

• bisc.zip (last updated Nov. 29 2012)
  

Additional material

• arXiv paper
  

The first example

The instructions below assume you have Sage on your machine and have downloaded the archive bisc.zip and unzipped it in you home directory. Start Sage and upload the notebook BiSC_load_example.sws. The first cell in the notebook will load files containing the algorithm, helper functions and examples. The contents of the next cell should be

'''
Load an example from examples.sage

gr_num             : Group number
ex_num             : Example number
largest_good_perms : The largest permutations that satisfy the property
largest_bad_perms  : The largest permutations that do not satisfy the property
cpus               : The number of cores to use. Set to 0 if you want Sage to
                     determine the number of available cores
'''

gr_num             = 0
ex_num             = 2
largest_good_perms = 8
largest_bad_perms  = 8
cpus               = 7

A, B = examples_for_bisc( gr_num, ex_num, largest_good_perms, largest_bad_perms, cpus )
    
size_of_subdicts(A)
				

Here we have chosen an example from Group 0, which contains examples of permutations that avoid a set of mesh patterns. Example nr. 2 will create the set of permutations avoiding the mesh patterns (12,{(0,0),(1,1),(2,2)}) and (12,{(0,2),(1,1),(2,0)}). We have chosen to create the permutations avoiding these two patterns up to length 8 (by setting largest_good_perms = 8). These are stored in the dictionary A. We also put the complement of these permutations up to length 8 (by setting (largest_bad_perms = 8) in the dictionary B. It is our goal below to "rediscover" these two patterns, just by looking at the permutations in the dictionaries A and B. Notice that you can also set the number of cpus Sage will try to use to do this. Set cpus = 0 if you want Sage to figure out the number of cpus on your system.

Now we run the first part of BiSC, where we mine for allowed patterns in the permutations from the dictionary A. Since we know that the permutations in A are the avoiders of two patterns of length 2, we set M = 2.

'''
Run the mine algorithm on the permutations in A

A      : The permutations created above
M      : The length of the longest patterns to search for
N      : The longest permutations in A to consider
report : Set to True if you want mine to tell you what it is doing
'''

M      = 2
N      = largest_good_perms
report = True

# Initializing a dictionary of good patterns that will be learned from A
goodpatts = dict()

ci, goodpatts = mine( A, M, N, report )
				

mine should find 11 allowed patterns of length 2. The next step is to run forb where we will hopefully generate the two patterns that we are looking for.

'''
Run the forb algorithm on the output from mine and generate
patterns of length at most M (should be at most the M from above)

ci        : The interval created by mine
goodpatts : The patterns found by mine
M         : The longest patterns to generate
report    : Set to True if you want forb to tell you what it is doing
'''

M      = 2
report = True
cpus   = 7

SG = forb( ci, goodpatts, M, report )

describe_bisc_output( SG )
				

Somewhat disappointingly we get four, instead of two, mesh patterns. Running the code in the next cell will display the patterns.

'''
If you want to see what the patterns look like run this
'''

show_multiple(dict_to_MeshPatts(SG),4,0.5)
				

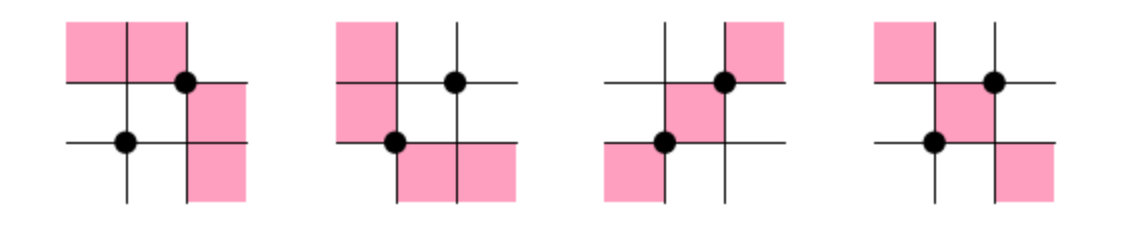
We will deal with this a little further down. Right now we can console ourselves with the fact that these four patterns correctly describe the permutations in the dictionary B.

'''
Run this to see if the output from forb actually describes the input permutations.
(We use the permutations in B to do this, so make sure you have enough of those)

SG              : The output from forb
L               : The longest permutations from B to use
B               : The permutations created above, that do not satisfy the property
stop_on_failure : If True then when a permutation in B that avoids the patterns
                  is found we stop immediately. If false we finish looking at
                  permutations of that length and output them
parallel        : If True then use more than one core
ncpus           : If set to 0 and parallel=True then Sage will use all available
                  cores. Otherwise pick the number of cores to use
'''

L               = largest_bad_perms
stop_on_failure = False
parallel        = True
ncpus           = 7
        
patterns_suffice( SG ,L , B, stop_on_failure, parallel, ncpus )
				

This should tell you that it goes through permutations of lengths 1...8 without reporting any trouble. Now we come to the part where we get rid of the unnecessary patterns.

'''
The output from forb is sometimes redundant, i.e., some patterns are not really
necessary. Run this to see what will work as bases

SG              : The output from forb
2nd parameter   : The longest permutations from B to use
bm              : The longest patterns from SG to use
4th parameter   : The permutations created above, that do not satisfy the property under consideration
M               : The same M as above. Don't change
report          : Set to true if you want to know what's going on
detailed_report : Set to true if you want to know everything that's going on
limit_monitors  : Whether to only consider bases of a given maximum length. Set to 0 if you want to allow any length
'''

bm              = 5
report          = True
detailed_report = False
limit_monitors  = 2

bases, dict_numbs_to_patts = clean_up( SG, min(SG.keys())+1, bm, min(SG.keys()), M, report, detailed_report, limit_monitors )

print ""
print "The sizes of the bases are:"
print map(lambda x : len(x), bases)
				

Here we set bm = 5 to use the permutations of length 1...5 from the dictionary B. We limit the size of bases we are interested in by setting limit_monitors = 2. As we had hoped we get a single base consisting of the two mesh patterns we were looking for.

'''
Run to see the patterns in a base
'''

base_nr = 0

b = map( lambda x : (x[0],x[1].list()), [dict_numbs_to_patts[b] for b in bases[base_nr]])

show_multiple(map( lambda x : MeshPattern(x[0],Set(x[1])), b),4,0.5)
				

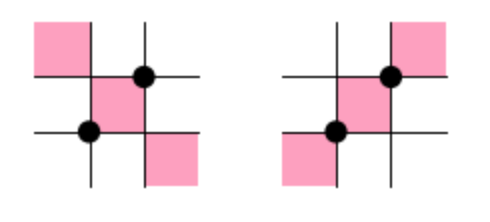
To be on the safe side, the last cell can be run to check whether these two mesh patterns correctly describe the permutations from the dictionary B.

More examples

To see more examples you have two choices: 1) Look inside the file examples.sage. At the beginning of the file there are comments describing what other examples you can load in the same way as we did above. 2) Open the Sage notebook BiSC_create_own_perms.sws where you can define your own dictionaries to run BiSC on.