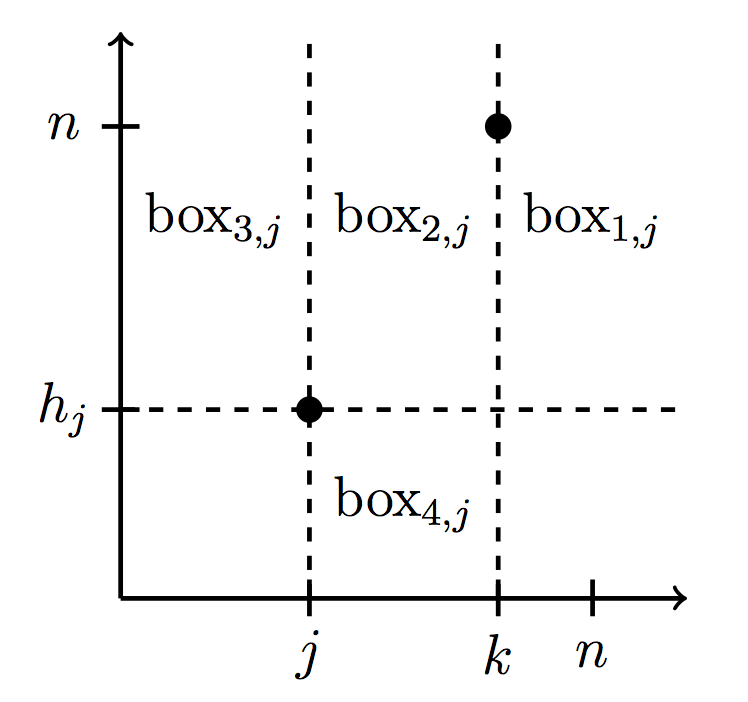We introduce and study new refinements of inversion statistics for permutations, such as k-step inversions, (the number of inversions with fixed position differences) and non-inversion sums (the sum of the differences of positions of the non-inversions of a permutation). We also provide a distribution function for non-inversion sums, a distribution function for k-step inversions that relates to the Eulerian polynomials, and special cases of distribution functions for other statistics we introduce, such as (\leq k)-step inversions and (k_1,k_2)-step inversions (that fix the value separation as well as the position). We connect our refinements to other work, such as inversion tops that are 0 modulo a fixed integer d, left boundary sums of paths, and marked meshed patterns. Finally, we use non-inversion sums to show that for every number n>34, there is a permutation such that the dot product of that permutation and the identity permutation (of the same length) is n.

Download the paper

• journal (open access)
  
• arXiv
  
• pdf